Menachem Magidor
| Menachem Magidor | |
|---|---|
Professor Menachem Magidor in Jerusalem, December 2006
|
|
| Born | January 24, 1946 Petah Tikva |
| Residence | Jerusalem, Israel |
| Nationality | Israel |
| Fields | Mathematician |
| Institutions | Hebrew University |
| Alma mater | Hebrew University |
| Doctoral advisor | Azriel Levy |
| Known for | Mathematical logic, Set theory, Large cardinal property |
Menachem Magidor (born 1946) is an Israeli mathematician who specializes in mathematical logic, in particular set theory. He served as President of the Hebrew University of Jerusalem.
Contents |
Biography
Menachem Magidor was born in Petah Tikva on January 24, 1946. He received his Ph.D. in 1973 from the Hebrew University. His thesis, On Super Compact Cardinals, was written under the supervision of Azriel Levy.[1]
Mathematical theories
Magidor obtained several important consistency results on powers of singular cardinals substantially developing the method of forcing. He generalized the Prikry forcing in order to change the cofinality of a large cardinal to a predetermined regular cardinal. He proved that the least strongly compact cardinal can be equal to the least measurable cardinal or to the least supercompact cardinal (but not at the same time). He proved consistent that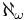 
is strong limit, but 
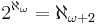. He even strengthened the condition that 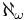is strong limit to that GCH holds below 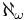. This constituted a negative solution to the singular cardinals hypothesis. Both proofs used the consistency of very large cardinals. With Matthew Foreman and Saharon Shelah they formulated and proved the consistency of Martin's maximum, a provably maximal form of Martin's axiom. Magidor also gave a simple proof of the Jensen and the Dodd-Jensen covering lemmas. He also proved that if 0# does not exist then every primitive recursive closed set of ordinals is the union of countably many sets in L.
Selected published works
- Magidor, Menachem (1977). "On the singular cardinals problem. I". Israel J. Math. 28 (1–2): 1–31. doi:10.1007/BF02759779.
- Magidor, Menachem (1977). "On the singular cardinals problem. II". Ann. Math. (2) (The Annals of Mathematics, Vol. 106, No. 3) 106 (3): 517–547. doi:10.2307/1971065. JSTOR 1971065.
- Foreman, Matthew; Magidor, Menachem and Shelah, Saharon (1988). "Martin's maximum, saturated ideals, and nonregular ultrafilters. I". Ann. Of Math. (2) (The Annals of Mathematics, Vol. 127, No. 1) 127 (1): 1–47. doi:10.2307/1971415. JSTOR 1971415.
- Foreman, Matthew; Magidor, Menachem and Shelah, Saharon (1988). "Martin's maximum, saturated ideals, and nonregular ultrafilters". Ann. Of Math. (2) (The Annals of Mathematics, Vol. 127, No. 3) 127 (3): 521–545. doi:10.2307/2007004. JSTOR 2007004.
- Foreman, Matthew and Magidor, Menachem (1995). "Large cardinals and definable counterexamples to the continuum hypothesis". Annals of Pure and Applied Logic 76 (1): 47–97. doi:10.1016/0168-0072(94)00031-W.